Le Théorème de Pythagore

Pour avoir le droit d'utiliser le théorème de Pythagore, il existe donc une condition d'utilisation impérative !

Autrement dit, utiliser le théorème avec un triangle quelconque donnera un résultat faux !

Nous vous présentons donc maintenant un triangle rectangle !

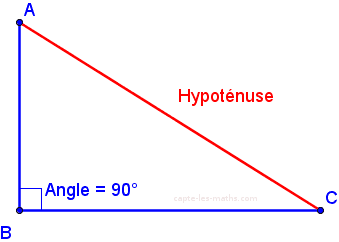
Le triangle ABC représenté est rectangle en B, car \(\widehat{B}=\widehat{ABC}=90°\), c'est à dire que l'angle formé par les côtés AB et BC vaut 90°. On l'appelle un angle droit.

Nous allons nous intéresser à un segment particulier de ce triangle rectangle, le coté AC. On lui a donné un nom : l'hypoténuse

Si vous voulez mieux connaître les triangles, consultez donc nos explications sur les Triangles et la façon de les noter.

Le mot hypoténuse sonne mal à nos oreilles, et vous vous demandez peut-être pourquoi employer un terme si bizarre. L'origine des mathématiques se trouve au fond des âges, c'est une capacité naturelle de l'homme. Dans la Grèce antique de grands mathématiciens (comme Pythagore ou Euclide) ont réfléchi sur les angles, les surfaces, les distances, leurs relations et la façon de les mesurer. Ils nous ont aussi laissé un peu de leur vocabulaire. On représentait souvent les angles « la pointe en haut », et on formait le triangle comme avec une corde que l'on tendait au-dessous (en grec « hupoteinousa pleura » signifie « côté se tendant sous les angles ») d'où le terme hypoténuse.

Nous avons plusieurs moyens pour la repérer :

Tous ces moyens sont bons pour repérer l'hypoténuse !

Classiquement, on formule le théorème ainsi :

Nous vous expliquons dans le Lexique, ce que sont le carré et la racine carrée d'un nombre.

Revenons à l'utilisation que l'on peut faire du théorème.

Comme d'habitude, ces mots vont s'éclairer avec un bon exemple :

Dans ces exercices de géométrie, le mieux est tracer la figure pour bien visualiser le problème posé :

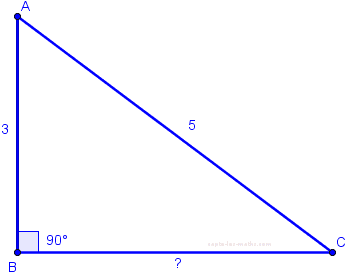
Le triangle ABC est rectangle en B, donc d'après le Théorème de Pythagore, nous avons la relation suivante entre les côtés du triangle : \[AC^2=AB^2+BC^2\]

Nous connaissons AB et AC, nous pouvons donc les remplacer dans l'équation par leurs valeurs : \[5^2=3^2+BC^2\] Ce qui nous donne : \[25=9+BC^2\] Et donc : \[\begin{align} BC^2 &=25−9 \\ &=16 \end{align}\] Soit : \[\begin{align} BC & =\sqrt{16} \\ & = 4 \end{align}\]

La longueur du côté BC est donc 4 cm.

Comme vous pouvez le constater, utiliser le théorème de Pythagore impose de connaître ce qu'est une Racine Carrée.

La réciproque de quelque chose, c'est l'opération inverse, celle qui permet de revenir au point de départ : nous savons aller de A jusqu'à B, la réciproque sera de savoir aller de B jusqu'à A.

La réciproque du théorème de Pythagore est aussi un théorème qui a été démontré.

Comprendre à quoi peut servir la réciproque du théorème est très simple en Français.

Dessinons ce triangle :

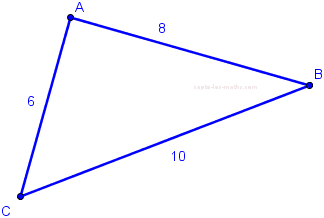
Nous voyons que CB est le côté le plus grand.

Si le triangle ABC est rectangle alors l'équation \[CB^2=AB^2+AC^2\] doit être vérifiée (nous devons avoir l'égalité des deux membres).

Nous vérifions que le carré du côté le plus grand est égal à la somme des carrés des deux autres côtés.

Nous allons donc calculer ce que vaut chaque membre de l'égalité : \[\begin{align} CB^2 &=10^2 \\ &=100 \end{align}\] Et d'autre part : \[\begin{align} AB^2 + AC^2 & =8^2+6^2 \\ & = 64 + 36 \\ & = 100 \end{align}\] Nous avons donc l'égalité des deux membres !

Puisque la relation \[CB^2=AB^2+AC^2\] est vraie, nous pouvons affirmer que le triangle ABC est rectangle en A. Et CB s'appelle donc l'hypoténuse.

Si ces opérations sur les équations ne vous sont pas familières, vous devriez étudier le fonctionnement des équations.

Ce qu'est la contraposée d'une proposition se comprend sur un exemple :

• Voici la proposition : si il fait beau alors le soleil brille

• Sa contraposée est : si le soleil ne brille pas alors il ne fait pas beau

Pour Pythagore cela nous donne :

• Théorème : si le triangle \(ABC\) est rectangle en \(B\) alors \(AC^2=AB^2+BC^2\)

• Contraposée : si \(AC^2\neq AB^2+BC^2\) alors le triangle \(ABC\) n'est pas rectangle en \(B\)

Allez on le répète : ne vous prenez pas la tête avec le mot contraposée mais retenez le résultat pour le théorème de Pythagore :

On peut dire aussi que : si la relation de Pythagore (entre la longueur des côtés d'un triangle) n'est pas vérifiée, on a le droit d'affirmer que ce triangle n'est pas rectangle.

Dessinons ce triangle :

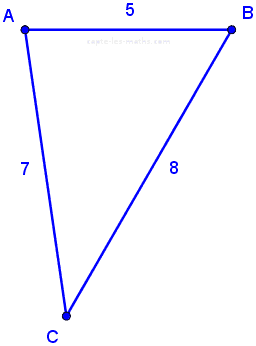
BC est le côté le plus grand, donc si le triangle ABC est rectangle alors l'équation \[BC^2=AB^2+AC^2\] doit être vérifiée (nous devons avoir l'égalité des deux membres).

Calculons chaque membre de l'égalité : \[\begin{align} BC^2 &=8^2 \\ &=64 \end{align}\] Et, \[\begin{align} AB^2 + AC^2 & =5^2+7^2 \\ & = 25 + 49 \\ & = 74 \end{align}\] Nous n'avons pas l'égalité des deux membres !

En appliquant la contraposée du théorème de Pythagore, nous pouvons affirmer que puisque \(BC\) est le côté le plus grand et que \(BC^2\neq AB^2+AC^2\), le triangle \(ABC\) n'est pas rectangle.

Quand Pythagore a travaillé sur la mesure des côtés du triangle rectangle, l'expression carré était pour lui quelque chose de tout à fait concret. Car quand on emploie le mot carré, ce n'est pas seulement une façon de parler : la surface d'un carré est égale à son côté multiplié par son côté, c'est à dire à son côté puissance 2. Nous disons maintenant à son côté au carré.
Ce que Pythagore a remarqué (et les Babyloniens avant lui) c'est que la surface du carré qui a pour côté l'hypoténuse est égale à l'addition des surfaces des carrés construits à partir des deux autres côtés.
Vous le visualiserez bien dans cette petite animation qui illustre le fonctionnement du théorème de Pythagore (ça rame parfois, mais ça vaut la peine d'insister).